前言

因为有个小可爱搞不清楚各种进制，正好我自己是学计算机的，既能帮自己梳理下知识，同时也可以给各位搞不清楚或模糊的读者朋友们进行参考。

学术有限，都是参考资料以及自己的一些见解而谈，有说错的地方可以指正！

有哪些进制？

常见的有二进制、八进制、十进制、十六进制等

十进制就是我们平常看到的各种数字运用于计算数学，

二进制、八进制与十六进制则是运用于计算机之中，是计算机的语言

八进制其实见到的也挺少的。

提一嘴，其实每个进制的加减乘除和十进制都是很像的，十进制是我们平常看到的数字，也就是所谓的逢十进一，所以其他进制也是一样。比如十六进制就是逢16进1等等，可以举一反三。

二进制

二进制是以2为基数代表系统的二进位制(binary)

特征：只有0和1 每一个数字被称为一个比特(bit) 8位一组（8bit比特 = 1bytes字节）范围是00000000(0) ~ 11111111(255)

计算机中，我们所能看到的很多信息都是机器通过二进制机器码转换而成的。它们只认识0和1（只是一种代表，不真代表只有0和1 A和B也是可以的），计算机以不同的方式呈现给人们看，因为二进制0与1若要进行转换非常繁琐。

计算

加减乘除

一般来说加法和减法见的比较多。

加法：
要注意[逢2进1] 跟十进制有点像。两个1相加则在下一个最高位+1

举例：100111+11010=100001
1 0 0 1 1 1
1 1 0 1 0
————————————
1 0 0 0 0 0 1

有四种情况： 0+0=0，0+1=1，1+0=1，1+1=10(0 进位为1)

两者相加有1则为1 两个1则为10 其余都为0

减法：
有四种情况：0－0=0，1－0=1，1－1=0，0－1=1

举例：1000001-11010=100111
1 0 0 0 0 0 1
1 1 0 1 0
————————————
0 1 0 0 1 1 1

乘法：
有四种情况： 0×0=0，1×0=0，0×1=0，1×1=1

除法：
有两种情况(除数只能为1)：0÷1=0，1÷1=1

运算可以看如下图：

二进制 –> 八进制

方法：取三合一法，即从二进制的小数点为分界点，向左（向右）每三位取成一位，接着将这三位二进制按权拼接，然后按顺序进行排列，小数点的位置不变，得到的数字就是我们所求的八进制数;

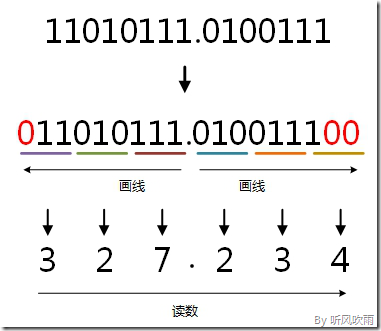
例：将二进制的11010111.0100111转换为八进制的步骤如下(从小数点开始往两边画,不足三位补0);

  1. 小数点前:

  111 = 7;

  010 = 2;

  11补全为011, 011 = 3;

  2. 小数点后:

  010 = 2;

  011 = 3;

  1补全为100，100 = 4;

读数: 读数从高位到低位，即11010111.0100111=327.234

二进制 –> 十进制

二进制转换成十进制为了方便讲解就举个例子来说明：

例：010110转为十进制

0 1 0 1 1 0

首先二进制8位一组，不足8位需要左边补0。看二进制从最右边看 以2为底数依次增加幂并乘以0或1 再把结果加在一起。

所以这一个转为十进制先补0为

0 0 0 1 0 1 1 0

再进行运算

0* 2^0(最右边的) + 1* 2^1 (右边前1位) + 1 * 2^2 (以此类推)+ 0 * 2^3 + 1 * 2^4 + 0 * 2^5 + 0 * 2^6 + 0 * 2^7

= 0 + 2 + 4 + 0 + 16 + 0 + 0 + 0 

= 22

只用转换有1的位置 因为有0的会被乘为0

二进制 –> 十六进制

取四合一法，即从二进制的小数点为分界点，向左（向右）每四位取成一位，接着将这四位二进制按权相拼接，然后按顺序进行排列，小数点的位置不变，得到的数字就是我们所求的十六进制数;

例：11010111转为十六进制

0111 = 7;

1101 = D;

读数: 读数从高位到低位，即11010111=D7

十进制

十进制就是我们平常看见的数字有0，1，2，3， 4， 5， 6， 7， 8， 9十个基本数字组成。

计算

十进制 –> 二进制

除2取余法，即每次将整数部分除以2，余数为该位权上的数，而商继续除以2，余数又为上一个位权上的数，这个步骤一直持续下去，直到商为0为止;

读数: 从最后一个余数读起，一直到最前面的一个余数;

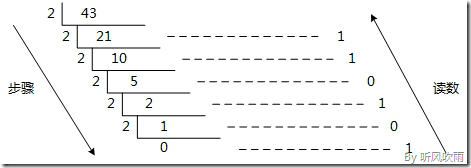
例：将十进制的(43)转换为二进制的步骤如下;

  1. 将商43除以2，商21余数为1;

  2. 将商21除以2，商10余数为1;

  3. 将商10除以2，商5余数为0;

  4. 将商5除以2，商2余数为1;

  5. 将商2除以2，商1余数为0; 

  6. 将商1除以2，商0余数为1;

读数: 因为最后一位是经过多次除以2才得到的，因此它是最高位，读数字从最后的余数向前读，101011，即(43)=(101011)

十进制 –> 八进制

方法1：

除8取余法，即每次将整数部分除以8，余数为该位权上的数，而商继续除以8，余数又为上一个位权上的数，这个步骤一直持续下去，直到商为0为止;

读数: 从最后一个余数起，一直到最前面的一个余数;

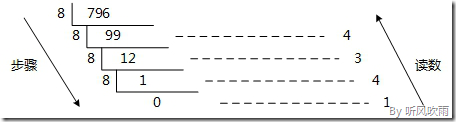
例：将十进制的796转换为八进制的步骤如下;

  1. 将商796除以8，商99余数为4;

  2. 将商99除以8，商12余数为3;

  4. 将商12除以8，商1余数为4;

  5. 将商1除以8，商0余数为1;

 读数: 因为最后一位是经过多次除以8才得到的，因此它是最高位，读数字从最后的余数向前读，1434，即796=1434

方法2：

先将十进制转换成二进制，然后将二进制又转换成八进制;

十进制 –> 十六进制

方法1：

除16取余法，即每次将整数部分除以16，余数为该位权上的数，而商继续除以16，余数又为上一个位权上的数，这个步骤一直持续下去，直到商为0为止;

读数: 从最后一个余数起，一直到最前面的一个余数;

例：十进制796转为十六进制

  1. 将商796除以16，商49余数为12，对应十六进制的C;

  2. 将商49除以16，商3余数为1;

  3. 将商3除以16，商0余数为3;

读数: 因为最后一位是经过多次除以16才得到的，因此它是最高位，读数字从最后的余数向前读，31C，即 796=31C

方法2：
先将十进制转换成二进制，然后将二进制又转换成十六进制;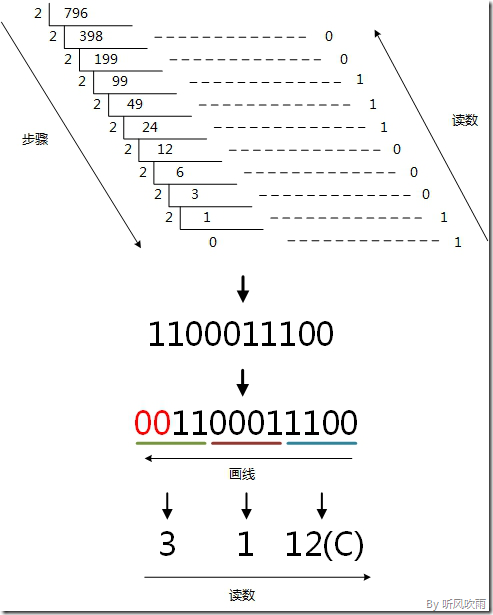

十六进制

十六进制（简写为hex或下标16）是一种基数为16的计数系统，是一种逢16进1的进位制。

十六进制可以更方便的表示二进制，计算机硬件是0101二进制的，16进制刚好是2的倍数，更容易表达一个命令或者数据

同时，十六进制也可以表达颜色，4个16进制位可以表达好几百万的颜色

特征：由数字0~~9和字母A、B、C、D、E、F（a、b、c、d、e、f）表示，其中:A~~F表示10~15 4个二进制可表达1个十六进制

计算

加减乘除

加法和减法与十进制相同逢16进1

加法：

200AD881
00000050
————————
200AD8D1

8+5 = 13 < 16 所以不用在下一位进1

减法：

其实大体与十进制相同，要注意字母的转换，借位

51-40=11 C8-3A=8E FD-88=75

乘法：

逢16进1 与十进制相同

除法：

向高位借1，即借到“16”

十六进制 –> 二进制

二进制和十六进制编码对应表

二进制(B)    十六进制(O)
0000            0
0001            1
0010            2
0011            3
0100            4
0101            5
0110            6
0111            7
1000            8
1001            9
1010            A
1011            B
1100            C
1101            D
1110            E
1111            F

取一分四法，即将一位十六进制数分解成四位二进制数，用四位二进制按权相加去凑这位十六进制数，小数点位置照旧;

例：0xDF 转为二进制

D = 11 = 1101

F = 15 = 1111

DF = 11011111

十六进制 –> 八进制

方法：先将十六进制转换为二进制，然后再将二进制转换为八进制，小数点位置不变;

例：将十六进制的D7转换为八进制的步骤如下：

  1. 十六进制D7转换成二进制;

    D = 1101;

    7 = 0111;

  2. 得到11010111, 再转换成八进制;

    111 = 7
    
    010 = 2

    11补0 为011 = 3

  读数: 读数从高位到低位，327，即D7=327

十六进制 –> 十进制

方法: 十六进制数从低位到高位（即从右往左）计算，第0位的权值是16的0次方，第1位的权值是16的1次方，第2位的权值是16的2次方，依次递增下去，把最后的结果相加的值就是十进制的值了;

例： 0x2B转为十进制

第1位 B * 16^0 = 11;

第2位 2 * 16^1 = 32;

读数: 把结果值相加，11+32=43，即2B=43

八进制

八进制是一种以8为基数的计数法。一些编程语言中常常以数字0开始表明该数字是八进制。八进制的数和二进制数可以按位对应（八进制一位对应二进制三位），因此常应用在计算机语言中。

实际上，由于十六进制一位可以对应4位二进制数字，用十六进制来表示二进制较为方便。因此，八进制的应用不如十六进制。有一些程序设计语言提供了使用八进制符号来表示数字的能力，而且还是有一些比较古老的Unix应用在使用八进制。

特征：采用0~7八个数字逢8进1。八进制一位对应二进制三位。

计算

加减乘除

与十进制的算法相同只是逢8进1

加法：

例：355 + 157 = 534

355
157
———
534

5+7，为12大于8，所以结果为 4并且向前进一

5+5，为10，再加上上一位进的一，11大于8，结果为 3并向前进 1

3+1，再加上上一位进的一，结果为 4+1=5

所以结果：355 + 157 = 534

减法：

例如：534 - 157 = 355

534
157
———
355

4-7，不够向前借一位加8，即为（4+8）-7，结果为 5

3-5，因为3已经被借了一变为2，2-5不够再向前借一位加 8，即为（2+8）-5，结果为 5

5-1，5被借了一，即为4-1，结果为 3

所以结果：534 - 157 = 355

乘法：

例如：221 x 147

221
147
———
1767
904
221
———
35127

所以结果 221 * 147 = 35127

除法：

如下图：（画图手写可太难了）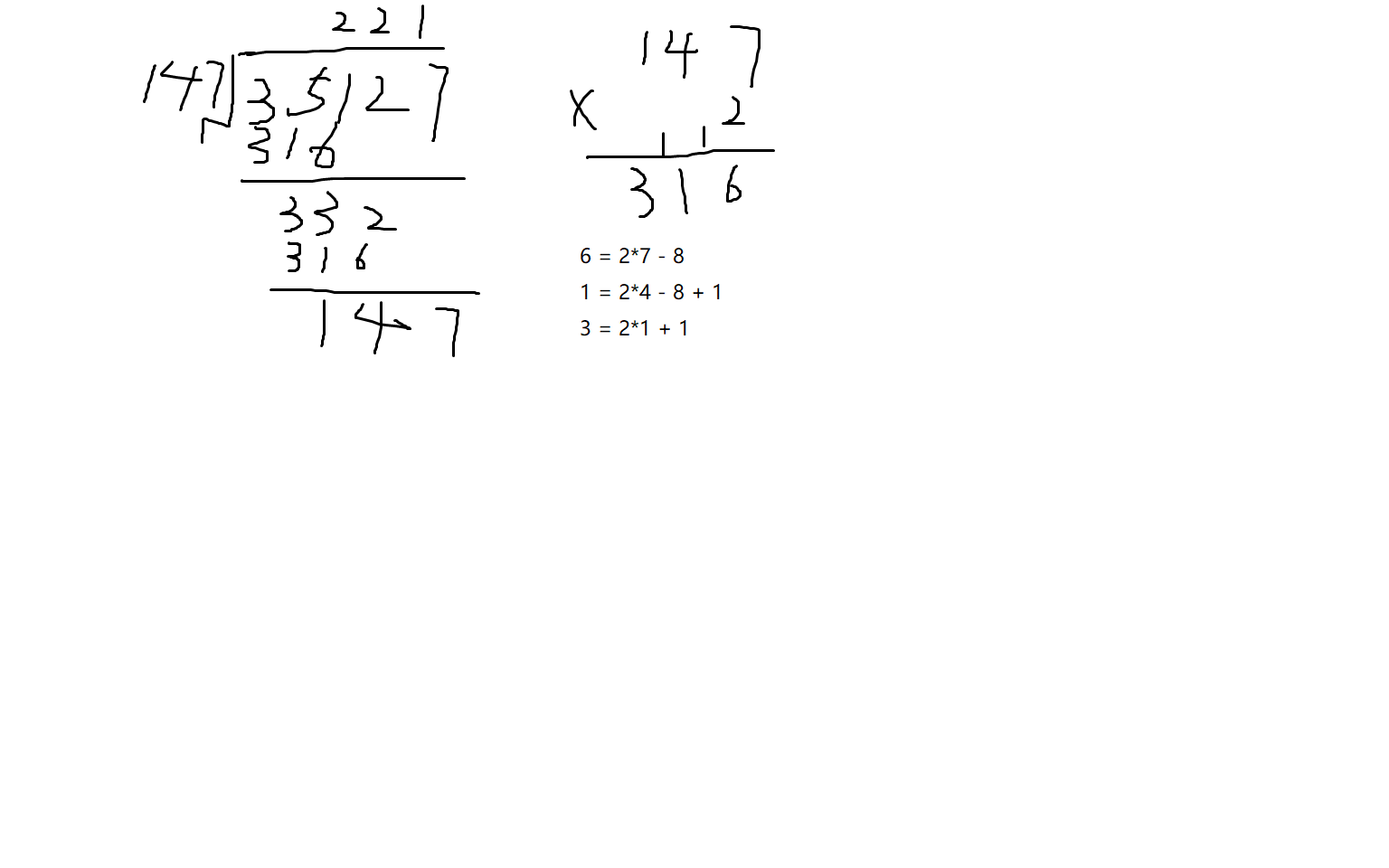

八进制 –> 二进制

二进制和八进制编码对应表

二进制(B)    八进制(O)
000                0
001                1
010                2
011                3
100                4
101                5
110                6
111                7

方法：
取一分三法，即将一位八进制数分解成三位二进制数，用三位二进制按权相加去凑这位八进制数，小数点位置照旧

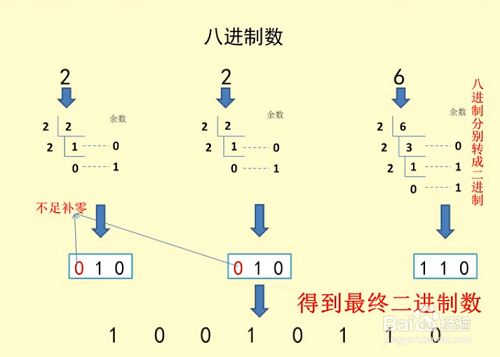
八进制 –> 十进制

方法：
八进制数从低位到高位（即从右往左）计算，第0位的权值是8的0次方，第1位的权值是8的1次方，第2位的权值是8的2次方，依次递增下去，把最后的结果相加的值就是十进制的值了

  八进制就是逢8进1，八进制数采用 0～7这八数来表达一个数;
  例：将八进制的53转换为十进制

  第1位 3 * 8^0 = 3;

  第2位 5 * 8^1 = 40;

  读数: 把结果值相加，3+40=43，即53=43

八进制 –> 十六进制

方法：
先将八进制转换为二进制，然后再将二进制转换为十六进制，小数点位置不变

例：将八进制的327转换为十六进制的步骤如下：

  1. 八进制327转换成二进制;

       3 = 011;

    2 = 010;

    7 = 111;
  2. 得到011010111, 再转换成十六进制;

    0111 = 7;
    
    1101 = D;

  读数: 读数从高位到低位，D7，即327=D7